Knuth 在 2018 圣诞节上竟然戴着锁链跳舞?
引言
我在翻看 Knuth 最近的更新时,发现他每年圣诞节都会跑到斯坦福去做演讲,去年我也写(ken)了他的圣诞三重奏, 2023年圣诞的主题是 Dancing Cell,我瞅了一眼,发现要搞懂这个就得先弄明白 Dancing Link。这个算法我早在 2011 年就听说过,只晓得用它解数独超快,但具体咋做、我也从来没实现过。所以呀,我决定先从 Dancing Link 开始学起。
精准匹配 Exact Cover
有一类超有趣的问题叫精确匹配问题,给定一个 n*m 的 01 矩阵,然后要求选出若干行,得让每行中包含的 1 恰好在每列出现一次。 例如下面的矩阵:
| 0 | 0 | 1 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 |
可以看出选择第1、4和5行可以恰好让每列有且只有一个1那这问题咋解呢? 一般来说就是那种朴素的搜索,选定一行再选定一行, 一直到没法接着选或者把所有 1 都收集齐为止。不过这个时间复杂度可不是多项式时间, 如果不考虑剪枝,那选法可有 2^n 种呢!
Algorithm X
早在2000年Knuth就提出了Algorithm X 算法用来解决精准匹配问题, 面对上面的矩阵,算法过程像这样:
- 当矩阵不是空时,选定含有1个数最少的那一列,这里是第一列
- 删除这列
| 0 | 1 | 0 | 1 | 1 | 0 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 1 |
- 把这列中有 1 的行选出来,这里就是第2和4行
- 对于选出来的行,直接删掉
| 0 | 1 | 0 | 1 | 1 | 0 | |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 1 |
- 并且将这些行中 1 所在的列也删掉,这里第 2 行的第一、四和七列以及第 4 行的第一和四列是 1,将这些列删掉(第一列已经被删了)
| 0 | 1 | 1 | 1 | |||
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | |||
| 1 | 0 | 0 | 0 | |||
| 0 | 0 | 1 | 0 |
- 将剩下的矩阵整理好(矩阵从6*7变成了4*4),从第1步开始继续,直到矩阵为空
| 0 | 1 | 1 | 1 |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
下面来解释解释为啥删除行和列能解决匹配问题。实际上这个过程相当于在为后面的选择剪枝, 选出来第 2 行,删掉第 2 行这很好理解。删掉第 2 行中是 1 的列, 意思就是不用再考虑这些列。涉及到的第 4 行被删, 是因为它和第 2 行都有第一列的 1,它就不可能再被选到了, 不然第一列就有两个 1 喽。如果不删掉第 4 行其他的 1, 那假如有一次要选第四列(这里虽然第四列在第 2 行时被删了,但比如这里是第五列第六列结论都成立),那就有可能选到第 4 行。但第 4 行选到也会因为第一列有 1 导致有两个 1 而失败,所以第 4 行的其他 1 所在列也要删。
双向链表 Doubly Linked Lists
双向链表大家在数据结构课上都学过吧。咱们也可以把上面的矩阵转换成链表来表示。当是 1 的时候就加入一个链表节点,是 0 就不加,每个节点都要记录自己在矩阵里的坐标。这里可不光是左右双向,还是上下双向。再给每一列增加一个头指针,就像这样:
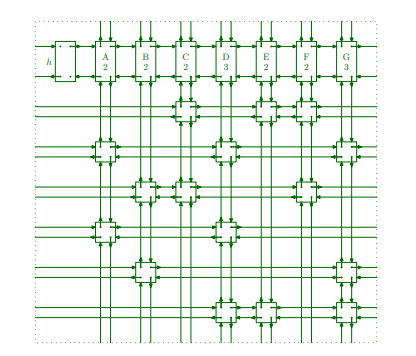 对于水平或竖直方向的链表移除操作非常简单:
对于水平或竖直方向的链表移除操作非常简单:
x.right.left = x.left
x.left.right = x.right
之所以说移除不说删除也是因为x并不会真的释放掉,它的数据还会保留, 稍后会再加回来,增加操作就是:
x.right.left = x
x.left.right = x
Dancing Link
一切准备就绪,接下来将这些合在一起就是Dancing Link了,
Dancing Link是一个奇妙的建模方法,
它不仅可以解数独,如果建模得当还能解决各种拼图问题,比如
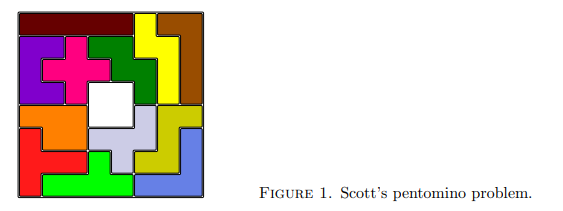
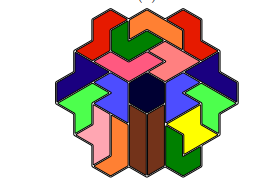
不过我觉得这篇文章我已经讲的够多了, 我决定留到下一篇再说。
图片均出自Dancing Link 论文
